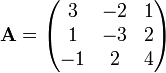Matrice à diagonale dominante

En algèbre linéaire, une matrice carrée à coefficients réels ou complexes est dite à diagonale dominante lorsque le module de chaque terme diagonal est supérieur ou égal à la somme des modules des autres termes de sa ligne. Si ${\displaystyle A=(a_{i,j})_{(i,j)\in [\![1,n]\!]^{2}}}$, on a alors :

${\displaystyle \forall i\in [\![1,n]\!],\ |a_{i,i}|\geq \sum _{j=1 \atop j\neq i}^{n}|a_{i,j}|.}$

De la même manière, A est dite à diagonale strictement dominante lorsque :

${\displaystyle \forall i\in [\![1,n]\!],\ |a_{i,i}|>\sum _{j=1 \atop j\neq i}^{n}|a_{i,j}|.}$

Lemme de Hadamard

Le « lemme de Hadamard » est un cas particulier du théorème de Gerschgorin. Inversement, il peut servir de lemme pour démontrer ce dernier.

Si ${\displaystyle A=(a_{i,j})_{(i,j)\in [\![1,n]\!]^{2}}}$ est une matrice à diagonale strictement dominante alors A est inversible.

Corollaire

Soit A une matrice hermitienne.

• Si A est à diagonale dominante alors, elle est positive si (et seulement si) ses coefficients diagonaux sont des réels positifs ou nuls.
• Si A est à diagonale strictement dominante alors, elle est définie positive si (et seulement si) ses coefficients diagonaux sont des réels strictement positifs.

Notes et références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Diagonally dominant matrix » (voir la liste des auteurs).

Articles connexes

• Méthode de Jacobi
• Méthode de Gauss-Seidel

• Portail de l’algèbre